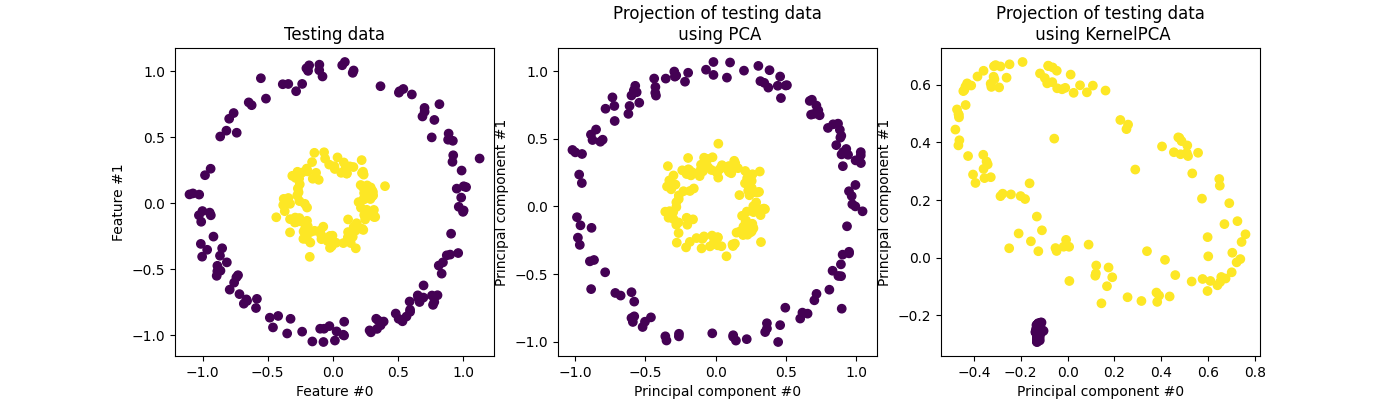
AdaMax

In Adam, the update rule for individual weights is scaling their gradients inversely proportional to the norm of the past and current gradients.

The L2 norm can be generalized to the norm.

Such variants generally become numerically unstable for large , which is why and norms are most common in practice. However, in the special case where we let , a surprisingly simple and stable algorithm emerges.

To avoid confusion with Adam, we use  to denote the infinity norm-constrained :

We can now plug into the Adam update equation replacing to obtain the AdaMax update rule:

Code

• AdaMax Numpy Implementation

Resources

• https://arxiv.org/abs/1412.6980
• https://ruder.io/optimizing-gradient-descent/index.html#adamax
• https://keras.io/api/optimizers/adamax/