Linear Discriminant Analysis (LDA)
Published on: November 9, 2021
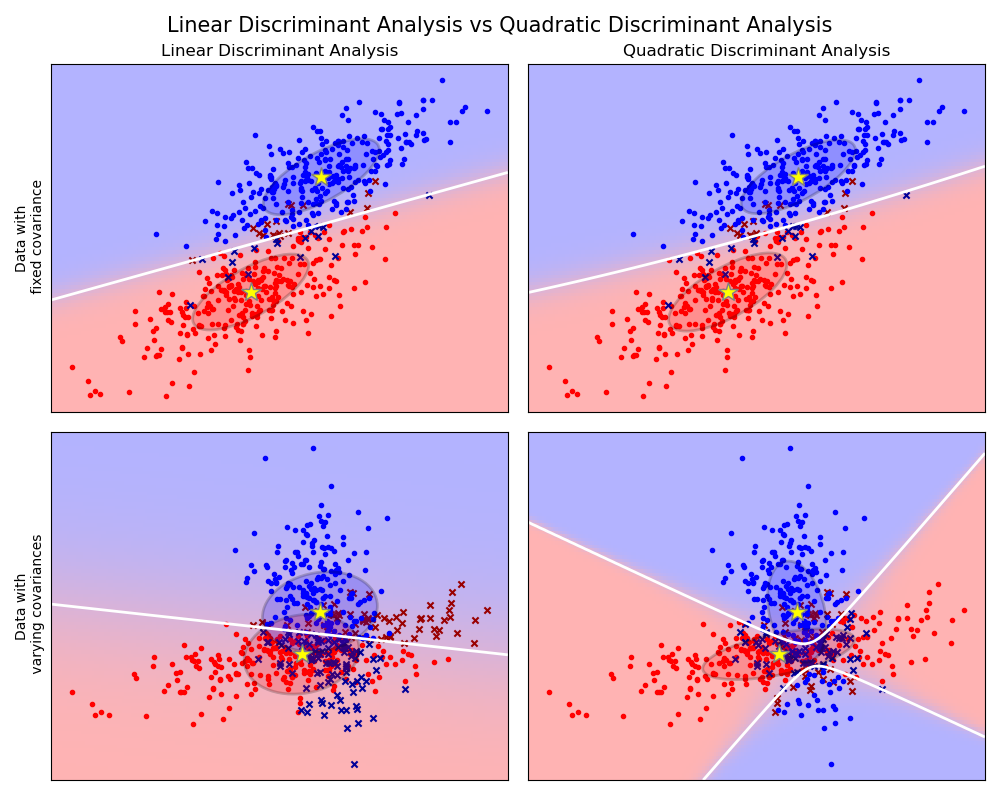
Table of Content
Linear Discriminant Analysis (LDA) is a dimensionality reduction technique commonly used for supervised classification problems. The goal of LDA is to project the dataset onto a lower-dimensional space while maximizing the class separability.
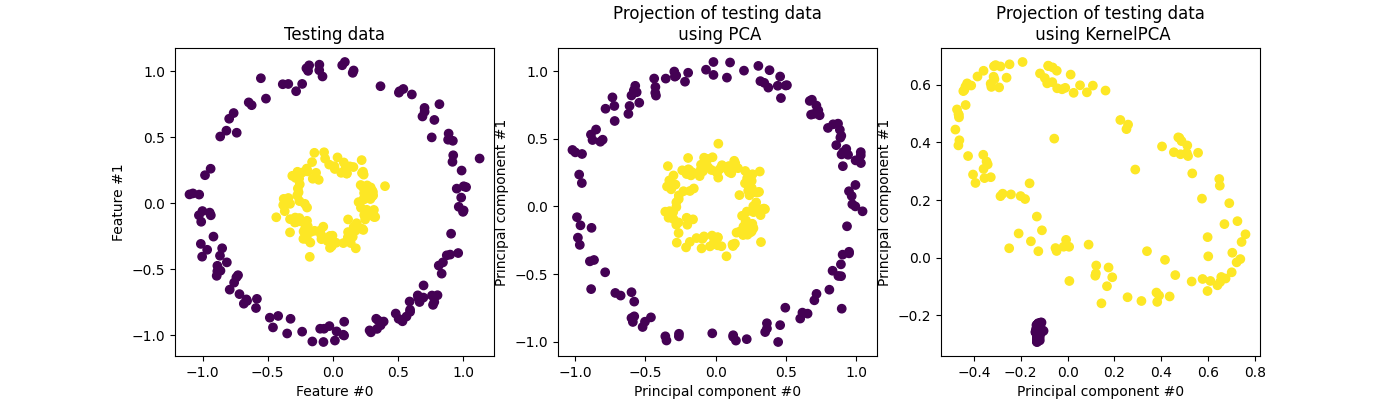
LDA is very similar to Principal Component Analysis (PCA), but there are some important differences. PCA is an unsupervised algorithm, meaning it doesn't need class labels
LDA can be performed in 5 steps:
- Compute the mean vectors for the different classes from the dataset.
- Compute the scatter matrices (in-between-class and within-class scatter matrices).
- Compute the eigenvectors and corresponding eigenvalues for the scatter matrices.
- Sort the eigenvectors by decreasing eigenvalues and choose k eigenvectors with the largest eigenvalues.
- Use this eigenvector matrix to transform the samples onto the new subspace.
Computing the mean vectors
First, calculate the mean vectors for all classes inside the dataset.
Computing the scatter matrices
After calculating the mean vectors, the within-class and between-class scatter matrices can be calculated.
Within-class scatter matrix
where
and
Alternativeley the class-covariance matrices can be used by adding the scaling factor
Between-class scatter matrix
where
Calculate linear discriminants
Next, LDA solves the generalized eigenvalue problem for the matrix
Select linear discriminants for the new feature subspace
After calculating the eigenvectors and eigenvalues, we sort the eigenvectors from highest to lowest depending on their corresponding eigenvalue and then choose the top
Transform data onto the new subspace
After selecting the