Kernel PCA

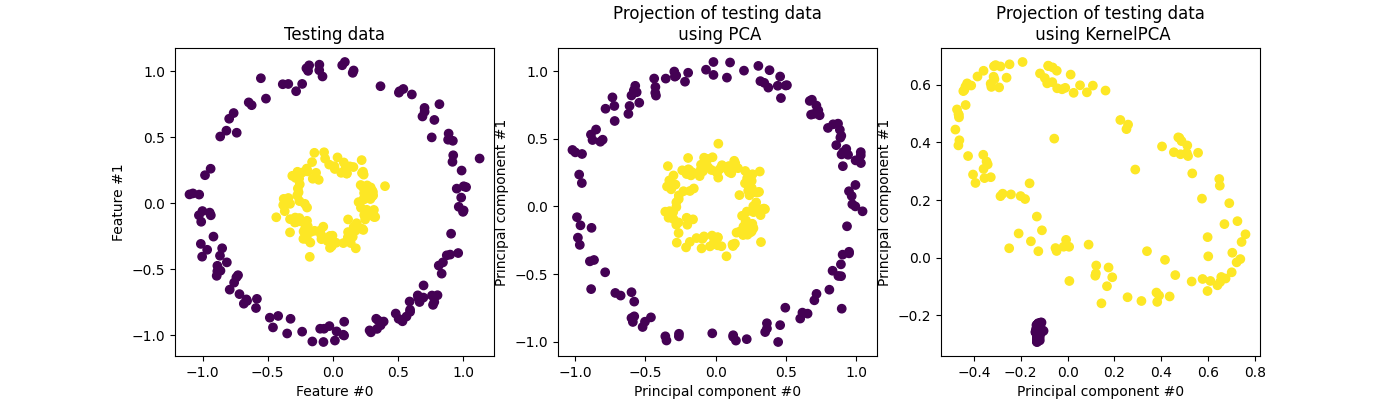
Kernel PCA is an extension of PCA that allows for the separability of nonlinear data by making use of kernels. The basic idea behind it is to project the linearly inseparable data onto a higher dimensional space where it becomes linearly separable.

Kernel PCA can be summarized as a 4 step process [1]:

1. Construct the kernel matrix from the training dataset

2. If the projected dataset doesn’t have zero mean use the Gram matrix to substitute the kernel matrix .

3. Use to solve for the vector .

4. Compute the kernel principal components

[1] Kernel Principal Component Analysis and its Applications in Face Recognition and Active Shape Models

Resources

• Kernel Principal Component Analysis and its Applications in Face Recognition and Active Shape Models
• Kernel tricks and nonlinear dimensionality reduction via RBF kernel PCA
• PCA and kernel PCA explained
• What are the advantages of kernel PCA over standard PCA?